Rancangan Bujur Sangkar Latin: Pengertian, Contoh, dan Aplikasi

Pada percobaan biologi, sering kali pengamatan dilakukan secara berulang pada satuan percobaan yang sama.  Pada kasus tersebut, mungkin saja beberapa perlakuan akan menghasilkan pengaruh yang berbeda selama percobaan berlangsung, konsekuensinya, mungkin akan mempengaruhi respons yang diamati pada periode yang berbeda.  Sehingga respons mungkin merupakan fungsi dari perlakuan pada periode tertentu.  Salah satu cara untuk menghilangkan galat percobaan tersebut adalah dengan cara memasukkan waktu/periode pengamatan ke dalam perlakuan.  Dengan demikian, di sini terdapat dua arah pengelompokan (double blocking), pertama berdasarkan kelompok pada percobaan dasar, dan kedua kelompok dari waktu pengamatan, sehingga rancangannya menjadi RBSL. 

RBSL di mana perlakuan dalam urutan numerik atau alpabetis di tempatkan pada baris dan  kolom pertama disebut dengan Rancangan Dasar (standar).  Gambar berikut merupakan rancangan dasar untuk ukuran 2x2, 3x3, dan 4x4.  Penambahan ukuran (perlakuan) secara cepat akan meningkatkan jumlah kemungkinan rancangan dasar.  Jumlah rancangan dasar yang mungkin dibentuk adalah (# of standard squares) (K!) (K - 1)! di mana k adalah jumlah perlakuan. Sebagai contoh, apabila k =4, maka kemungkinan rancangan dasar yang bisa dibentuk adalah (4).(4!).(3!) = 576 kemungkinan.

4x4

A

B

C

D

A

B

C

D

2x2

B

A

D

C

B

C

D

A

A

B

C

D

B

A

C

D

A

B

B

A

D

C

A

B

D

A

B

C

3x3

A

B

C

D

A

B

C

D

A

B

C

B

D

A

C

B

A

D

C

B

C

A

C

A

D

B

C

D

A

B

C

A

B

D

C

B

A

D

C

B

A

Gambar 9.    Rancangan dasar RBSL untuk ukuran 2x2, 3x3, dan 4x4.

Keuntungan rancangan bujur sangkar latin :

1. Mengurangi keragaman galat melalui penggunaan dua buah pengelompokan
2. Pengaruh perlakuan dapat dilakukan untuk percobaan berskala kecil
3. Analisis relatif mudah
4. Baris atau kolom bisa juga digunakan untuk meningkatkan cakupan dalam pengambilan kesimpulan

Kelemahan rancangan bujur sangkar latin :

1. Banyaknya baris, kolom dan perlakuan harus sama, sehingga semakin banyak perlakuan, satuan percobaan yang diperlukan juga semakin banyak.
2. Apabila banyaknya kelompok bertambah besar, galat percobaan per satuan percobaan juga cenderung meningkat.
3. Asumsi modelnya sangat mengikat, yaitu bahwa tidak ada interaksi antara sembarang dua atau semua kriteria , yaitu baris, kolom dan perlakuan.
4. Pengacakan yang diperlukan sedikit lebih rumit daripada pengacakan rancangan-rancangan sebelumnya.
5. Derajat bebas galatnya yang lebih kecil dibanding dengan rancangan lain yang berukuran sama, akan menurunkan tingkat ketelitian, terutama apabila jumlah perlakuannya berukuran kecil.
6. Memerlukan pengetahuan/pemahaman dasar dalam menyusun satuan percobaan yang efektif.
7. Apabila ada data hilang, meskipun jumlahnya tidak terlalu banyak, maka hasil analisisnya diragukan karena perlakuan menjadi tidak seimbang. 

Setiap perlakuan muncul sekali di setiap baris  dan sekali pada setiap kolom.  Pertama, pilih rancangan dasar yang sesuai dengan ukurannya, kemudian lakukan pengacakan pada arah baris, dan selanjutnya pengacakan pada arah kolom.

Misal terdapat 4 perlakuan A, B, C, D. 

1. Kita pilih rancangan dasar ukuran 4x4.

Baris\Kolom	1	2	3	4
1	A	B	C	D
2	B	A	D	C
3	C	D	B	A
4	D	C	A	B

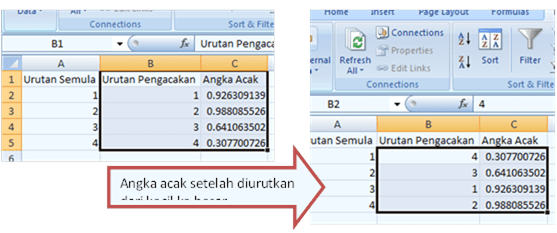
2. Pengacakan pada posisi baris.  Misal pengacakan dengan menggunakan fungsi Rand() pada MS Excel (cara pengacakan secara detail dengan bantuan MS Excel dapat dilihat pada pengacakan RAL).  Dari proses pengacakan tersebut kita mendapatkan urutan baru 4, 3, 1, 2. Artinya, baris yang asalnya ada diposisi ke-1(urutan semula) berubah menjadi posisi 4 (Urutan pengacakan), beris ke-2 menjadi baris ke-3, dst.
   

Dari hasil pengacakan pada posisi baris tersebut kita mendapatkan hasil sebagai berikut:

Baris\Kolom	1	2	3	4
4	D	C	A	B
3	C	D	B	A
1	A	B	C	D
2	B	A	D	C

3. Dengan cara yang sama, kita lakukan pengacakan untuk posisi kolom. Misalkan kita mendapatkan urutan pengacakan: 2, 1, 4, 3.  Artinya, kolom ke-1 menjadi kolom ke-2, kolom ke-2 menjadi kolom ke-1, dst. Dari hasil pengacakan pada posisi kolom tersebut kita mendapatkan hasil sebagai berikut:

Baris\Kolom	2	1	4	3
2	C	D	B	A
4	D	C	A	B
1	B	A	D	C
3	A	B	C	D

 

Setelah selesai melakukan pengacakan pada arah baris dan kolom, kemudian buat Denah percobaan seperti pada gambar berikut.

C	D	B	A
D	C	A	B
B	A	D	C
A	B	C	D

Gambar 10.  Denah percobaan RBSL 

Model Linier Rancangan Bujur Sangkar Latin

Model linier rancangan bujur sangkar latin  adalah:

$$Y_{ijk}=\mu+\beta_i+\kappa_j+\tau_k+\varepsilon_{ijk}$$

μ       = rataan umum

β_i          = pengaruh baris ke-i

κ_j          = pengaruh kolom ke-j

τ_k          = pengaruh perlakuan ke-k

ε_ijk       = pengaruh acak dari baris ke-i, kolom ke-k dan perlakuan ke-k

i = 1,2, …,r ;           j = 1,2, …,r ;           k = 1,2, …,r

Asumsi:

Pengaruh perlakuan tetap	Pengaruh perlakuan acak
$\sum{\beta_i\ \ =\ \sum{\kappa_j=}\sum\tau_k}\ =\ 0\ ;\ \ \ \ \ \varepsilon_{ijk}\overset{bsi}{\sim}N(0,\sigma^2)$	$\begin{matrix}\beta_i\overset{bsi}{\sim}N(0,{\sigma_\beta}^2);\ \ \ \ \ \ \kappa_j\overset{bsi}{\sim}N(0,{\sigma_j}^2);\ \ \ \ \ \\\tau_k\overset{bsi}{\sim}N(0,{\sigma_\tau}^2);\ \ \ \ \ \ \ \ \ \varepsilon_{ijk}\overset{bsi}{\sim}N(0,\sigma^2)\\\end{matrix}$

 

Hipotesis:

Hipotesis yang Akan Diuji:	Pengaruh perlakuan tetap	Pengaruh perlakuan acak
H0	Semua τk = 0 (k = 1, 2, …, r)	στ2 = 0 (tidak ada keragaman dalam populasi perlakuan)
H1	Tidak semua τk = 0 (k = 1, 2, …, r)	στ2 > 0 (ada keragaman dalam populasi perlakuan)

 

Analisis Ragam:

Parameter	Penduga
$$\mu$$	$$\hat{\mu}=\ \bar{Y}..$$
$$\beta_i$$	$${\hat{\beta}}_{i\ }\ =\ Y_{i.}-\bar{Y}..$$
$$\kappa_j$$	$${\hat{\kappa}}_j\ =\ {\bar{Y}}_{.j}-\bar{Y}..$$
$$\tau_k$$	$${\hat{\tau}}_k\ =\ {\bar{Y}}_k-\bar{Y}..$$
$$\varepsilon_{ij(k)}$$	$${\hat{\varepsilon}}_{ij}=Y_{ij}-{\overline{Y}}_{i.}-{\overline{Y}}_{.j}-{\overline{Y}}_k+2{\overline{Y}}_{..}$$

Persamaan Jumlah kuadrat untuk model linier Y_ij(k) = μ + β_i + κ_j + τ_(k) + ε_ij  adalah sebagai berikut:

$$\sum_{i,j}^{r}{({\overline{Y}}_{ij}-{\overline{Y}}_{..})^2=r\sum_{i=1}^{r}{({\overline{Y}}_{i.}-{\overline{Y}}_{..})^2+r\sum_{j=1}^{r}{({\overline{Y}}_{.j}-{\overline{Y}}_{..})^2}+r\sum_{k=1}^{r}{({\overline{Y}}_k-{\overline{Y}}_{..})^2}+\sum_{i,j}^{k}{(Y_{ij}-{\overline{Y}}_{i.}-{\overline{Y}}_{.j}+-{\overline{Y}}_k+2{\overline{Y}}_{..})^2}}}$$

atau,      JKT =       JKBaris        +     JK Kolom            +      JKP        +   JKG

Rumus jumlah kuadrat dalam rancangan bujur sangkar latin adalah sebagai berikut :

	Definisi	Pengerjaan
FK	$$\frac{Y..^2}{r^2}$$	$$\frac{Y..^2}{r^2}$$
JKT	$$\sum_{i,j}{\left(Y_{ij}-\bar{Y}..\right)^2=\sum_{i,j}{{Y_{ij}}^2-\frac{Y..^2}{r^2}}}$$	$$\sum_{i,j}{{Y_{ij}}^2-FK}$$
JKBaris	$$ r\sum_{i}\left({\bar{Y}}_{i.}-\bar{Y}..\right)^2=\sum_{i}\frac{{Y_{i.}}^2}{r}-\frac{Y..^2}{r^2}$$	$$\sum_{i}\frac{{Y_{i.}}^2}{r}-FK$$
JKKolom	$$ r\sum_{j}\left({\bar{Y}}_{.j}-\bar{Y}..\right)^2=\sum_{j}\frac{{Y_{.j}}^2}{r}-\frac{Y..^2}{r^2}$$	$$\sum_{j}\frac{{Y_{.j}}^2}{r}-FK$$
JKP	$$ r\sum_{k}\left({\bar{Y}}_k-\bar{Y}..\right)^2=\sum_{k}\frac{{Y_k}^2}{r}-\frac{Y..^2}{r^2}$$	$$\sum_{k}\frac{{Y_k}^2}{r}-FK$$
JKG	$$\sum_{i,j}{(Y_{ij}-{\bar{Y}}_{i..}-{\bar{Y}}_{.j.}-{\bar{Y}}_k+2{\bar{Y}}_{..})^2}$$	JKT – JKBaris – JKKolom – JKP

Tabel 4.1. Analisis Ragam Rancangan Bujur Sangkar Latin

Sumber Keragaman	Derajat Bebas	Jumlah Kuadrat	Kuadrat Tengah	Fhitung	E(KT)
	(DB)	(JK)	(KT)		Semua faktor tetap	Semua faktor acak
Baris	r-1	JKBaris	JKBaris/(r-1)	$$\frac{KTBaris}{KTG}$$	$$\sigma^2+r\frac{\sum{\beta_i}^2}{r-1}$$	$$\sigma^2+r{\sigma^2}_\alpha$$
Kolom	r-1	JKKolom	JKKolom/(t-1)	$$\frac{KTKolom}{KTG}$$	$$\sigma^2+r\frac{\sum{\kappa_j}^2}{r-1}$$	$$\sigma^2+r{\sigma^2}_\beta$$
Perlakuan	r-1	JKP	JKP/(r-1)	$$\frac{KTP}{KTG}$$	$$\sigma^2+r\frac{\sum{\tau_k}^2}{r-1}$$	$$\sigma^2+{\sigma^2}_\tau$$
Galat	(r-1)(r-2)	JKG	JKG/(r-1)(r-2)		$$\sigma^2$$	$$\sigma^2$$
Total	r2 –1

Statistik uji yang sesuai untuk menguji hipotesis di atas :  $ F=\frac{KTP}{KTG}$

Kaidah keputusan apabila galat jenis I sebesar α, apabila F≤ F_{tabel [α; r-1, (r-1)(r-2)]} maka keputusannya adalah terima H₀ dan sebaliknya. F_{tabel [α; r-1, (r-1)(r-2)]} adalah nilai F tabel yang luas di sebelah kanannya sebesar α dengan derajat bebas pembilang r-1 dan derajat bebas penyebut (r-1)(r-2).

Adakalanya kita ingin menguji ada atau tidaknya pengaruh peubah pengelompokan. Apabila peubah pengelompokan bersifat tetap, maka uji hipotesisnya adalah sebagai berikut : 

Uji hipotesis untuk peubah pengelompokan baris :

H₀           :     Semua β_i = 0                                

H₁           :     Tidak semua β_i  = 0

dengan statistik uji  $ F=\frac{KTBaris}{KTG}$

Uji Hipotesis untuk peubah pengelompokan kolom :

H₀           :     Semua κ_j = 0                                

H₁           :     Tidak semua κ_j  = 0

Statistik uji : $ F=\frac{KTKolom}{KTG}$

Kaidah keputusan untuk pengaruh baris dan kolom : apabila F≤ F_{tabel [α; r-1, (r-1)(r-2)]} terima H₀ dan sebaliknya.

Galat Baku

Galat baku (Standar error) untuk perbedaan di antara rata-rata perlakuan dihitung dengan formula berikut:

$$S_{\bar{Y}}=\sqrt{\frac{2KTG}{t}}$$

Contoh penerapan

Untuk memudahkan pemahaman prosedur perhitungan sidik ragam RBSL berikut ini disajikan contoh kasus beserta perhitungan sidik ragamnya.  Tabel berikut adalah Layout dan data hasil percobaan RBSL ukuran 4x4 untuk data hasil pipilan jagung hibrida (A, B, dan D) dan penguji (C) (Gomez & Gomez, 1995 hal 34).

No. Baris	Hasil Pipilan (t ha-1)				Jumlah Baris
	1	2	3	4
1	1.640 (B)	1.210 (D)	1.425 (C)	1.345 (A)	5.620
2	1.475 (C)	1.185 (A)	1.400 (D)	1.290 (B)	5.350
3	1.670 (A)	0.710 (C)	1.665 (B)	1.180 (D)	5.225
4	1.565 (D)	1.290 (B)	1.655 (A)	0.660 (C)	5.170
Jumlah Kolom	6.350	4.395	6.145	4.475
Jumlah Umum					21.365

            

Langkah-langkah dalam menyusun Perhitungan Sidik Ragam:

1. Susun data seperti pada tabel di atas (sesuai dengan layout percobaan di lapangan), sertakan pula penjelasan kode perlakuannya.
2. Hitung jumlah baris (B) dan kolom (B) serta jumlah Umum (G) seperti pada contoh tabel di atas.
3. Hitung Jumlah dan Rataanya untuk masing-masing Perlakuan.

	Jumlah	Rataan
A	5.855	1.464
B	5.885	1.471
C	4.270	1.068
D	5.355	1.339

4. Hitung Jumlah Kuadrat untuk semua sumber keragaman.
   

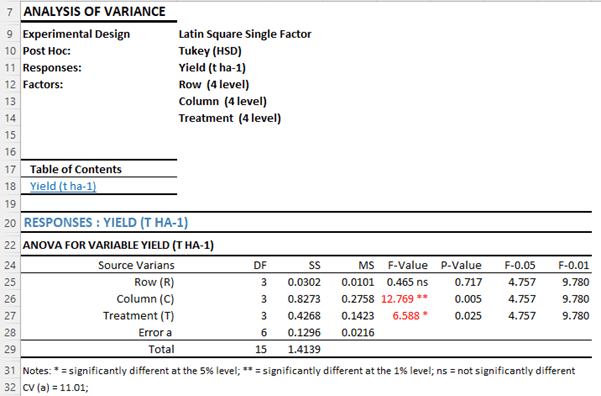
5. Susun Tabel Sidik Ragamnya dan Nilai F-tabel :

Sumber Keragaman	DB	JK	KT	Fhitung	F0.05
Baris	3	0.030154	0.010051	0.465393	4.757
Kolom	3	0.827342	0.275781	12.7691*	4.757
Perlakuan	3	0.426842	0.142281	6.58783*	4.757
Galat	6	0.129585	0.021598
Total	15	1.413923

Post-Hoc (Tukey HSD)

Langkah 1: Hitung nilai HSD:

• Tentukan nilai KTG dan derajat bebasnya yang diperoleh dari Tabel Analisis Ragam.
  • KTG = 0.021598
  • ν = db = 6
• Tentukan nilai kritis dari tabel wilayah nyata student. 
  • Ada tiga parameter yang dibutuhkan untuk menentukan nilai q_α, yaitu taraf nyata (α), p = banyaknya perlakuan yang akan dibandingkan, dan derajat bebas galat (db).  Pada contoh ini, p = 4, nilai db = 6 (lihat db galat pada tabel Analisis Ragamnya) dan α = 0.05. Selanjutnya, tentukan nilai q_{0.05(4, 6)}.
  • Untuk mencari nilai q_{0.05(6, 24)} kita dapat melihatnya pada tabel Sebaran studentized range pada taraf nyata α = 0.05 dengan p = 4 dan derajat bebas (v)= 6.  Perhatikan gambar berikut untuk menentukan q-tabel.
    
  • Dari tabel tersebut kita dapatkan nilai q_{0.05(6, 24)} = 4.90
• Hitung nilai Tukey HSD dengan menggunakan formula berikut:
  $\begin{matrix}\omega=q_\alpha(p,\nu)\sqrt{\frac{KTG}{t}}\\=4.90\times\sqrt{\frac{0.021598}{4}}\\=0.36\\\end{matrix}$
• Kriteria pengujian:
  • Bandingkan nilai mutlak selisih kedua rata-rata yang akan kita lihat perbedaannya dengan nilai HSD dengan kriteria pengujian sebagai berikut:
    $$ Jika\ \ \left|\mu_i-\mu_j\right|\ \ \left\langle\ \ \begin{matrix}>HSD_{0.05}maka\ hasil\ uji\ menjadi\ nyata\\\le HSD_{0.05}maka\ hasil\ uji\ tidak\ nyata\\\end{matrix}\right.$$

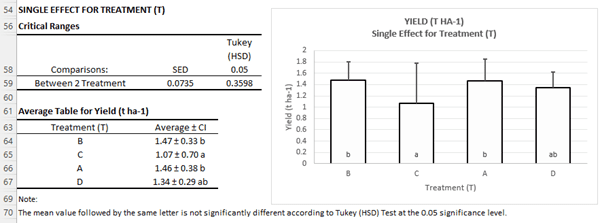
Langkah 2: Urutkan tabel rata-rata perlakuan dari kecil ke besar atau sebaliknya. Buat Tabel matriks selisih di antara rata-rata perlakuan dan bandingkan dengan nilai pembanding (Tukey HSD = 0.36).

		(C)	(D)	(A)	(B)	Notasi
Perlakuan	Rata-rata	1.068	1.339	1.464	1.471
(C)	1.068	0.000				a
(D)	1.339	0.271 tn	0.000			ab
(A)	1.464	0.396 *	0.125 tn	0.000		b
(B)	1.471	0.404 *	0.133 tn	0.007 tn	0.000	b

Keterangan: abaikan garis merah, karena sudah terwakili oleh garis ke dua (b)

Perhitungan dengan SmartstatXL Excel Add-In

Tabel Analisis Ragam

Tabel Uji Lanjut

Hasil perhitungan dengan menggunakan Software SPSS V.16.

No. Baris	Hasil Pipilan (t ha-1)
	1	2	3	4
1	1.640 (B)	1.210 (D)	1.425 (C)	1.345 (A)
2	1.475 (C)	1.185 (A)	1.400 (D)	1.290 (B)
3	1.670 (A)	0.710 (C)	1.665 (B)	1.180 (D)
4	1.565 (D)	1.290 (B)	1.655 (A)	0.660 (C)

Buat list datanya seperti berikut:

Baris	Kolom	Perlakuan	Hasil
1	1	(B)	1.640
2	1	(C)	1.475
3	1	(A)	1.670
4	1	(D)	1.565
1	2	(D)	1.210
2	2	(A)	1.185
3	2	(C)	0.710
4	2	(B)	1.290
1	3	(C)	1.425
2	3	(D)	1.400
3	3	(B)	1.665
4	3	(A)	1.655
1	4	(A)	1.345
2	4	(B)	1.290
3	4	(D)	1.180
4	4	(C)	0.660

Model:

UNIANOVA hasil BY baris kolom perlakuan

  /METHOD=SSTYPE(3)

  /INTERCEPT=INCLUDE

  /POSTHOC=perlakuan(TUKEY LSD)

  /CRITERIA=ALPHA(0.05)

  /DESIGN=baris kolom perlakuan.

Output

Tests of Between-Subjects Effects
Dependent Variable:hasil
Source	Type III Sum of Squares	df	Mean Square	F	Sig.
Corrected Model	1.284a	9	.143	6.607	.016
Intercept	28.529	1	28.529	1320.944	.000
baris	.030	3	.010	.465	.717
kolom	.827	3	.276	12.769	.005
perlakuan	.427	3	.142	6.588	.025
Error	.130	6	.022
Total	29.943	16
Corrected Total	1.414	15
a. R Squared = .908 (Adjusted R Squared = .771)

Post Hoc

hasil
	perlakuan	N	Subset
			1	2
Tukey HSDa	(C)	4	1.0675000000E0
	(D)	4	1.3387500000E0	1.3387500000E0
	(A)	4		1.4637500000E0
	(B)	4		1.4712500000E0
	Sig.		.138	.608
Means for groups in homogeneous subsets are displayed.  Based on observed means.  The error term is Mean Square(Error) = .022.
a. Uses Harmonic Mean Sample Size = 4.000.

Latihan

Petersons et. al (1951) melakukan suatu percobaan pada tanaman Turnip Green dengan menggunakan Rancangan Bujur Sangkar Latin.  Penimbangan kehilangan kandungan air (I, II, III, IV, V) dilakukan pada waktu/periode tertentu.  Data yang dihasilkan pada tabel berikut merupakan kandungan air-80 (persen) (ST, hal. 225).

Apabila kita perhatikan, pada percobaan tersebut terdapat dua pengelompokan, pertama berdasarkan tanaman, dan kedua berdasarkan waktu pengukuran kandungan air.

Tanaman (Baris)	Ukuran daun (A=terkecil, B=terbesar) (Kolom)
	A	B	C	D	E
1	6.67(V)	7.15(IV)	8.29(I)	8.95(III)	9.62(II)
2	5.40(II)	4.77(V)	5.40(IV)	7.54(I)	6.93(III)
3	7.32(III)	8.53(II)	8.50(V)	9.99(IV)	9.68(I)
4	4.92(I)	5.00(III)	7.29(II)	7.85(V)	7.08(IV)
5	4.88(IV)	6.16(I)	7.83(III)	5.83(II)	8.51(V)

Pengolahan data dengan menggunakan sofware Statistica V. 7.0:

Tabel Analisis Ragam

	Degr. of Freedom	Kandungan Air SS	Kandungan Air MS	Kandungan Air F	Kandungan Air p
Intercept	1	1297.296	1297.296	1924.799	1.28E-14
Tanaman	4	28.8853	7.221324	10.71428	0.000623
Ukuran Daun	4	23.70814	5.927034	8.793941	0.001483
Waktu	4	0.627256	0.156814	0.232665	0.914655
Error	12	8.087888	0.673991
Total	24	61.30858

Post-Hoc (Tukey HSD)

Tukey HSD test; variable Kandungan Air (RBSL_Torrie in ContohData.stw) Homogenous Groups, alpha = .05000 Error: Between MS = .67399, df = 12.000
	Perlakuan	Kandungan Air	1
5	IV	6.900000	****
3	III	7.206000	****
1	V	7.260000	****
4	I	7.318000	****
2	II	7.334000	****

 

Tukey HSD test; variable Kandungan Air (RBSL_Torrie in ContohData.stw) Homogenous Groups, alpha = .05000 Error: Between MS = .67399, df = 12.000
	Tanaman	Kandungan Air	1	2	3
2	2	6.008000	****
4	4	6.428000	****
5	5	6.642000	****	****
1	1	8.136000		****	****
3	3	8.804000			****

 

Tukey HSD test; variable Kandungan Air (RBSL_Torrie in ContohData.stw) Homogenous Groups, alpha = .05000 Error: Between MS = .67399, df = 12.000
	Ukuran Daun	Kandungan Air	1	2
1	A	5.838000	****
2	B	6.322000	****
3	C	7.462000	****	****
4	D	8.032000		****
5	E	8.364000		****