Contoh dan Analisis Rancangan Petak-Petak Terbagi (Split-Split Plot)

Contoh Penerapan

Percobaan dibidang pertanian ingin mempelajari pengaruh dari tiga faktor yaitu, pemupukan Nitrogen (A), Manajemen terhadap tanaman (B) dan Jenis Varietas (C) terhadap hasil produksi padi (ton/ha). Faktor Nitrogen ditempatkan sebagai petak utama, Manajemen sebagai anak petak dan varietas sebagai anak-anak petak.

Tabel 44. Data Hasil Produksi Padi (ton/ha)

Perhitungan:

Langkah 1: Hitung Faktor Koreksi

$$ FK=\frac{Y....^2}{rabc}=\frac{(502.221)^2}{3\times3\times3\times3}=3113.90$$

Langkah 2: Hitung Jumlah Kuadrat Total

$$\begin{matrix}JKT=\sum_{i,j,k,l}{Y_{ijkl}}^2-FK\\=(3.320)^2+(3.864)^2+...+(9.320)^2-3113.90\\=189.71\\\end{matrix}$$

Analisis terhadap Petak Utama:

Data Total Petak Utama (Kelompok x Nitrogen)

Langkah 3: Hitung Jumlah Kuadrat Petak Utama

$$\begin{matrix}JK(PU)=\sum_{i,l}\frac{{Y_{i..l}}^2}{bc}-FK=\frac{\sum_{i,l}{(a_ir_l)^2}}{bc}-FK\\=\frac{(49.331)^2+(49.598)^2+...+(63.601)^2}{3\times3}-3113.900\\=37.36\\\end{matrix}$$

Langkah 4: Hitung Jumlah Kuadrat Kelompok

$$\begin{matrix}{JK}({K})=\sum_{{l}}\frac{{{Y}_{...{l}}}^\mathbf{2}}{{abc}}-{FK}=\frac{\sum_{{l}}{({r}_{l})^\mathbf{2}}}{{abc}}-{FK}\\=\frac{(\mathbf{166}.\mathbf{583})^\mathbf{2}+(\mathbf{171}.\mathbf{433})^\mathbf{2}+(\mathbf{164}.\mathbf{205})^\mathbf{2}}{\mathbf{3}\times\mathbf{3}\times\mathbf{3}}-\mathbf{3113}.\mathbf{90}\\=\mathbf{1}.\mathbf{005}\\\end{matrix}$$

Langkah 5: Hitung Jumlah Kuadrat Faktor A

$$\begin{matrix}{JK}({A})=\sum_{{i}}\frac{{{Y}_{{i}..}}^\mathbf{2}}{{rbc}}-{FK}=\frac{\sum_{{i}}{({a}_{i})^\mathbf{2}}}{{rbc}}-{FK}\\=\frac{(\mathbf{145}.\mathbf{387})^\mathbf{2}+(\mathbf{167}.\mathbf{949})^\mathbf{2}+(\mathbf{188}.\mathbf{885})^\mathbf{2}}{\mathbf{3}\times\mathbf{3}\times\mathbf{3}}-\mathbf{3113}.\mathbf{90}\\=\mathbf{35}.\mathbf{055}\\\end{matrix}$$

Langkah 6: Hitung Jumlah Kuadrat Galat Petak Utama (Galat a)

$$\begin{matrix}{JK}({Galat}\ {a})=\sum_{{i},{l}}\frac{{{Y}_{{i}..{l}}}^\mathbf{2}}{{bc}}-{FK}-{JKK}-{JKA}\\=\frac{\sum_{{i},{l}}{({a}_{i}{r}_{l})^\mathbf{2}}}{{bc}}-{FK}-{JKK}-{JKA}\\={JK}({PU})\ -\ {JK}({K})\ -\ {JK}({A})\ \\=\mathbf{37}.\mathbf{36}-\mathbf{1}.\mathbf{005}-\mathbf{35}.\mathbf{055}\\=\mathbf{1}.\mathbf{296}\\\end{matrix}$$

Analisis terhadap Anak Petak:

Data Total Anak Petak: Kelompok x Nitrogen x Manajemen (KAB)

Data Total Faktor Nitrogen x Manajemen (AB)

Langkah 7: Hitung Jumlah Kuadrat Anak Petak

$$\begin{matrix}JK(AP)=\sum_{i,j,l}\frac{{Y_{ij.l}}^2}{c}-FK\\=\frac{\sum_{i,j,l}{(a_ib_jr_l)^2}}{c}-FK\\=\frac{(14.776)^2+(14.522)^2+...+(23.629)^2}{3}-3113.900\\=63.07\\\end{matrix}$$

Langkah 8: Hitung Jumlah Kuadrat Faktor B

$$\begin{matrix}{JK}({B})=\sum_{{j}}\frac{{{Y}_{.{j}..}}^\mathbf{2}}{{rac}}-{FK}=\frac{\sum_{{j}}{({b}_{j})^\mathbf{2}}}{{rac}}-{FK}\\=\frac{(\mathbf{152}.\mathbf{086})^\mathbf{2}+(\mathbf{163}.\mathbf{598})^\mathbf{2}+(\mathbf{186}.\mathbf{537})^\mathbf{2}}{\mathbf{3}\times\mathbf{3}\times\mathbf{3}}-\mathbf{3113}.\mathbf{90}\\=\mathbf{22}.\mathbf{785}\\\end{matrix}$$

Langkah 9: Hitung Jumlah Kuadrat Interaksi AB

$$\begin{matrix}{JK}({AB})=\sum_{{i},{j}}\frac{{{Y}_{{ij}.}}^\mathbf{2}}{{rc}}-{FK}-{JKA}-{JKB}\\=\frac{\sum_{{i},{j}}{({a}_{i}{b}_{j})^\mathbf{2}}}{{rc}}-{FK}-{JKA}-{JKB}\\=\frac{(\mathbf{43}.\mathbf{864})^\mathbf{2}+(\mathbf{46}.\mathbf{575})^\mathbf{2}+...+(\mathbf{69}.\mathbf{069})^\mathbf{2}}{\mathbf{3}\times\mathbf{3}}-\mathbf{3113}.\mathbf{90}-\mathbf{35}.\mathbf{055}-\mathbf{22}.\mathbf{785}\\=\mathbf{0}.\mathbf{162}\\\end{matrix}$$

Langkah 10: Hitung Jumlah Kuadrat Galat Anak Petak (Galat b)

$$\begin{matrix}{JK}({Galat}\ {b})={JK}({AP})\ -\ {JK}({K})\ -\ {JK}({A})\ -\ {JK}({Galat}\ {a})\ -\ {JK}({B})\ -\ {JK}({AB})\ \ \\=\mathbf{63}.\mathbf{07}-\mathbf{1}.\mathbf{005}-\mathbf{35}.\mathbf{055}-\mathbf{1}.\mathbf{296}-\mathbf{22}.\mathbf{785}-\mathbf{0}.\mathbf{162}\\=\mathbf{2}.\mathbf{771}\\\end{matrix}$$

Analisis terhadap Anak-anak Petak:

Tabel Nitrogen x Varietas (AC)

Tabel Manajemen x Varietas (BC)

Tabel Nitrogen x Manajemen x Varietas (ABC)

Langkah 11: Hitung Jumlah Kuadrat Faktor C

$$\begin{matrix}{JK}({C})=\sum_{{k}}\frac{{{Y}_{..{k}.}}^\mathbf{2}}{{rab}}-{FK}\\=\frac{\sum_{{k}}{({c}_{k})^\mathbf{2}}}{{rab}}-{FK}\\=\frac{(\mathbf{136}.\mathbf{005})^\mathbf{2}+(\mathbf{159}.\mathbf{909})^\mathbf{2}+(\mathbf{206}.\mathbf{307})^\mathbf{2}}{\mathbf{3}\times\mathbf{3}\times\mathbf{3}}-\mathbf{3113}.\mathbf{90}\\=\mathbf{94}.\mathbf{649}\\\end{matrix}$$

Langkah 12: Hitung Jumlah Kuadrat Interaksi AC

$$\begin{matrix}{JK}({AC})=\sum_{{i},{k}}\frac{{{Y}_{{i}.{k}.}}^\mathbf{2}}{{rb}}-{FK}-{JK}({A})-{JK}({C})\\=\frac{\sum_{{i},{k}}{({a}_{i}{c}_{k})^\mathbf{2}}}{{rb}}-{FK}-{JK}({A})-{JK}({C})\\=\frac{(\mathbf{40}.\mathbf{618})^\mathbf{2}+(\mathbf{42}.\mathbf{873})^\mathbf{2}+...+(\mathbf{77}.\mathbf{074})^\mathbf{2}}{\mathbf{3}\times\mathbf{3}}-\mathbf{3113}.\mathbf{90}-\mathbf{35}.\mathbf{055}-\mathbf{94}.\mathbf{649}\\=\mathbf{3}.\mathbf{436}\\\end{matrix}$$

Langkah 13: Hitung Jumlah Kuadrat Interaksi BC

$$\begin{matrix}{JK}({BC})=\sum_{{j},{k}}\frac{{{Y}_{.{jk}.}}^\mathbf{2}}{{ra}}-{FK}-{JK}({B})-{JK}({C})\\=\frac{\sum_{{j},{k}}{({b}_{j}{c}_{k})^\mathbf{2}}}{{ra}}-{FK}-{JK}({B})-{JK}({C})\\=\frac{(\mathbf{40}.\mathbf{065})^\mathbf{2}+(\mathbf{43}.\mathbf{878})^\mathbf{2}+...+(\mathbf{77}.\mathbf{388})^\mathbf{2}}{\mathbf{3}\times\mathbf{3}}-\mathbf{3113}.\mathbf{90}-\mathbf{22}.\mathbf{785}-\mathbf{94}.\mathbf{649}\\=\mathbf{4}.\mathbf{240}\\\end{matrix}$$

Langkah 14: Hitung Jumlah Kuadrat Interaksi ABC

$$\begin{matrix}{JK}({ABC})=\sum_{{i},{j},{k}}\frac{{{Y}_{{ijk}.}}^\mathbf{2}}{{r}}-{FK}-{JK}({A})-{JK}({B})-{JK}({C})-\\{JK}({AB})-{JK}({AC})-{JK}({BC})\\=\frac{\sum_{{i},{j},{k}}{({a}_{i}{b}_{j}{c}_{k})^\mathbf{2}}}{{r}}-{FK}-{JK}({A})-{JK}({B})-{JK}({C})-\\{JK}({AB})-{JK}({AC})-{JK}({BC})\\=\frac{(\mathbf{11}.\mathbf{691})^\mathbf{2}+(\mathbf{16}.\mathbf{038})^\mathbf{2}+...+(\mathbf{27}.\mathbf{572})^\mathbf{2}}{\mathbf{3}}-\mathbf{3113}.\mathbf{90}-\mathbf{35}.\mathbf{055}-\mathbf{22}.\mathbf{785}-\mathbf{94}.\mathbf{649}-\\\mathbf{0}.\mathbf{162}-\mathbf{3}.\mathbf{436}-\mathbf{4}.\mathbf{240}\\=\mathbf{2}.\mathbf{363}\\\end{matrix}$$

Langkah 15: Hitung Jumlah Kuadrat Galat Anak-anak Petak (Galat c)

$$\begin{matrix}{JK}({Galat}\ {c})={JKT}-{semua}\ {komponen}\ {JK}\ {lainnya}\\={JKT}-{JK}({K})\ -\ {JK}({A})\ -\ {JK}({Galat}\ {a})\ -\ \\{JK}({B})\ -\ {JK}({AB})\ -\ {JK}({Galat}\ {b})-\ \\{JK}({C})\ -\ {JK}({AC})\ -\ {JK}({BC})\ -\ {JK}({ABC})\ \\=\mathbf{189}.\mathbf{709}-\mathbf{1}.\mathbf{005}-\mathbf{35}.\mathbf{055}-\mathbf{1}.\mathbf{296}-\\\mathbf{22}.\mathbf{785}-\mathbf{0}.\mathbf{162}-\mathbf{2}.\mathbf{771}-\\\mathbf{94}.\mathbf{649}-\mathbf{3}.\mathbf{436}-\mathbf{4}.\mathbf{240}-\mathbf{2}.\mathbf{363}\\=\mathbf{21}.\mathbf{947}\\\end{matrix}$$

Langkah 16: Buat Tabel Analisis Ragam beserta Nilai F-tabelnya

Tabel 45. Analisis Ragam RPPT Data Hasil Padi

Hitung koefisien keragaman:

$$\begin{matrix}kk(a)=\frac{\sqrt{KT(Galat\ a)}}{\bar{Y}...}\times100\%=\frac{\sqrt{0.324}}{6.200}\times100\%\\=9.18\%\\\end{matrix}$$

$$\begin{matrix}kk(b)=\frac{\sqrt{KT(Galat\ b)}}{\bar{Y}...}\times100\%=\frac{\sqrt{0.231}}{6.200}\times100\%\\=7.75\%\\\end{matrix}$$

$$\begin{matrix}kk(c)=\frac{\sqrt{KT(Galat\ c)}}{\bar{Y}...}\times100\%=\frac{\sqrt{0.6096}}{6.200}\times100\%\\=12.59\%\\\end{matrix}$$

jadi: kk (a) = 9.18 %; kk (b) = 7.75 %; kk (c) = 12.59 %;

Pada umumnya, koefisien keragaman petak utama > anak petak > anak-anak petak. Namun pada kasus di atas, tidak menunjukkan kondisi tersebut. Apabila hal tersebut sering terjadi, sebaiknya diskusikan dengan orang yang ahli dibidang statistik.

Langkah 17: Buat Kesimpulan

Dari Tabel Analisis Ragam tidak tampak bahwa pengaruh interaksi tidak signifikan, baik interaksi antara ketiga faktor (interaksi ABC) maupun interaksi antara dua faktor (AB, AC, BC), sehingga pemeriksaan pengaruh perlakuan dilanjutkan dengan pengaruh utamanya. Pengaruh utama (mandiri) dari ketiga faktor signifikan, sehingga perlu dilakukan pengusutan lebih lanjut untuk menentukan perbedaan di antara taraf rata-rata perlakuan.

Post Hoc

Berdasarkan analisis ragam, pengaruh interaksi tidak ada yang nyata, sedangkan ketiga pengaruh mandirinya nyata. Pengujian lanjut dilakukan terhadap pengaruh mandiri ketiga faktor tersebut.

Berikut adalah langkah pengujian Uji Lanjut dengan menggunakan LSD:

Kriteria pengujian:

Bandingkan nilai mutlak selisih kedua rata-rata yang akan kita lihat perbedaannya dengan nilai LSD dengan kriteria pengujian sebagai berikut:

$$ Jika\ \ \left|\mu_i-\mu_j\right|\ \ \left\langle\ \ \begin{matrix}>LSD_{0.05}maka\ hasil\ uji\ menjadi\ nyata\\\le LSD_{0.05}maka\ hasil\ uji\ tidak\ nyata\\\end{matrix}\right.$$

Perbandingan Rataan Faktor Nitrogen (A):

Untuk membandingkan dua rataan petak utama (Faktor Nitrogen), perlu ditentukan terlebih dahulu galat baku (s_y) dengan menggunakan formula:

$$s_{\bar{y}}=\sqrt{\frac{2KT(Galat\ \ a)}{rbc}}$$

Tentukan nilai t-student pada taraf nyata α =5% dengan derajat bebas galat a = 4:

t_{(0.05/2; 4)} = 2.776

Hitung nilai LSD:

$$\begin{matrix}LSD=t_{0.05/2;4}\cdot s_{\bar{Y}}\\=t_{0.05/2;4}\cdot\sqrt{\frac{2KT(Galat\ \ a)}{rbc}}\\=2.776\times\sqrt{\frac{2(0.32399)}{3\times3\times3}}=2.776\times0.15492\\=0.430\ \ kg\\\end{matrix}$$

Bandingkan selisih rata-rata perlakuan dengan nilai LSD = 0.430 kg. Nyatakan berbeda apabila selisih rata-ratanya lebih besar dibandingkan dengan nilai LSD. Hasilnya adalah sebagai berikut:

Perbandingan Rataan Faktor Manajemen (B):

Untuk membandingkan dua rataan anak petak (Faktor Manajemen), perlu ditentukan terlebih dahulu galat baku (s_y) dengan menggunakan formula:

$$s_{\bar{y}}=\sqrt{\frac{2KT(Galat\ \ b)}{rac}}$$

Tentukan nilai t-student pada taraf nyata α =5% dengan derajat bebas galat b = 12:

t_{(0.05/2; 12)} = 2.179

Hitung nilai LSD:

$$\begin{matrix}LSD=t_{0.05/2;12}\cdot s_{\bar{Y}}\\=t_{0.05/2;12}\cdot\sqrt{\frac{2KT(Galat\ \ b)}{rac}}\\=2.179\times\sqrt{\frac{2(0.23094)}{3\times3\times3}}=2.179\times0.13079\\=0.285\ \ kg\\\end{matrix}$$

Bandingkan selisih rata-rata perlakuan dengan nilai LSD = 0.285 kg. Nyatakan berbeda apabila selisih rata-ratanya lebih besar dibandingkan dengan nilai LSD. Hasilnya adalah sebagai berikut:

Perbandingan Rataan Faktor Varietas (C):

Untuk membandingkan dua rataan anak-anak petak (Faktor Varietas), perlu ditentukan terlebih dahulu galat baku (s_y) dengan menggunakan formula:

$$s_{\bar{y}}=\sqrt{\frac{2KT(Galat\ \ c)}{rab}}$$

Tentukan nilai t-student pada taraf nyata α =5% dengan derajat bebas galat c = 36:

t_{(0.05/2; 36)} = 2.0281

Hitung nilai LSD:

$$\begin{matrix}LSD=t_{0.05/2;36}\cdot s_{\bar{Y}}\\=t_{0.05/2;36}\cdot\sqrt{\frac{2KT(Galat\ \ c)}{rab}}\\=2.0281\times\sqrt{\frac{2(0.60965)}{3\times3\times3}}=2.0281\times0.2125\\=0.4310\ \ kg\\\end{matrix}$$

Bandingkan selisih rata-rata perlakuan dengan nilai LSD = 0.4310 kg. Nyatakan berbeda apabila selisih rata-ratanya lebih besar dibandingkan dengan nilai LSD. Hasilnya adalah sebagai berikut:

Perhitungan dengan menggunakan SmartstatXL Excel Add-In

Anova:

Post Hoc

Pengaruh Mandiri:

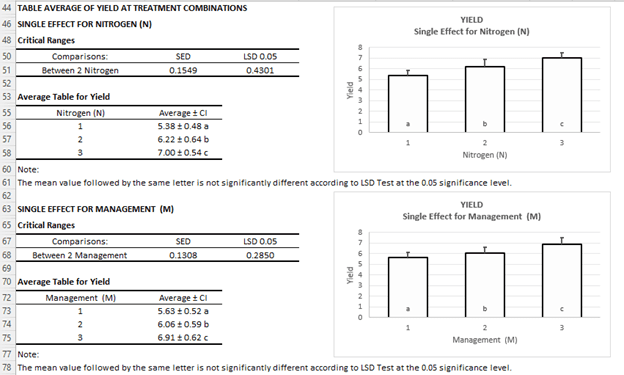
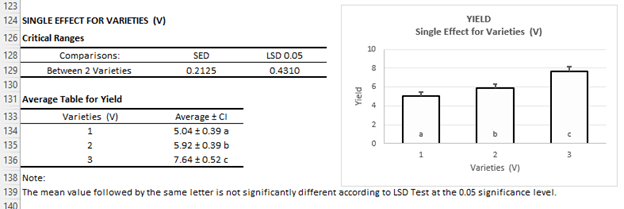
Pengaruh Interaksi (tidak signifikan)

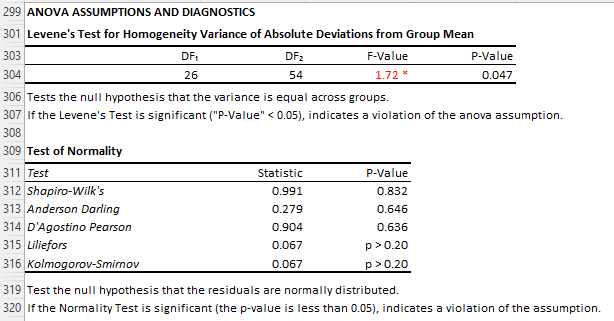
Asumsi Anova: