Sidebar Menu
Main Menu
Statistika
Statistika adalah cabang ilmu matematika terapan yang berfokus pada pengumpulan, pengukuran, klasifikasi, perhitungan, penjelasan, sintesis, analisis, dan interpretasi data. Di dalam kategori Statistika pada website Smartstat, Anda akan menemukan berbagai artikel yang membahas aspek-aspek penting dari statistika, baik deskriptif maupun inferensial. Artikel-artikel ini mencakup berbagai topik, mulai dari dasar-dasar statistika seperti pengertian statistika, populasi dan sampel, variabel dan data, skala pengukuran variabel; statistika deskriptif termasuk pengertian statistika deskriptif, ukuran pemusatan data, ukuran penyebaran, contoh perhitungan skewness dan kurtosis, dan distribusi frekuensi; eksplorasi data yang mencakup analisis data eksploratif, stemplot, dan pengenalan box-plot; korelasi dan regresi; uji t Student yang mencakup uji t-student, uji-t 2 populasi dengan ragam homogen, uji t-student 2 populasi dengan ragam heterogen, dan uji t berpasangan; serta beberapa uji non-parametrik seperti uji McNemar dan uji Wilcoxon untuk data berpasangan.
Artikel-artikel ini dirancang untuk membantu Anda memahami konsep-konsep penting dalam statistika dan bagaimana menerapkannya dalam penelitian Anda. Setiap artikel disajikan dengan penjelasan yang jelas dan mudah dipahami, menjadikan kategori Statistika ini sebagai sumber belajar yang berharga bagi siapa saja yang ingin memperdalam pengetahuan mereka tentang statistika.

- Detail
- Ditulis oleh Ade Setiawan
- Kategori: Statisika Deskriptif
Ukuran penyebaran (Measures of Dispersion) atau ukuran keragaman pengamatan dari nilai rata-ratanya disebut simpangan (deviation/dispersi). Terdapat beberapa ukuran untuk menentukan dispersi data pengamatan, seperti jangkauan/rentang (range), simpangan kuartil (quartile deviation), simpangan rata-rata (mean deviation), dan simpangan baku (standard deviation).
Ukuran tendensi sentral (mean, median, mode) merupakan nilai pewakil dari suatu distribusi frekuensi, tetapi ukuran tersebut tidak memberikan gambaran informasi yang lengkap mengenai bagaimana penyebaran data pengamatan terhadap nilai sentralnya. Ukuran tendensi sentral saja tidak cukup untuk menggambarkan distribusi frekuensi. Selain itu kita harus memiliki ukuran persebaran data pengamatan.
- Dilihat: 182535

- Detail
- Ditulis oleh Ade Setiawan
- Kategori: Analisis Data Eksploratif
Analisis data eksploratif (Exploratory Data Analysis – EDA) merupakan metode eksplorasi data dengan menggunakan teknik aritmatika sederhana dan teknik grafis dalam meringkas data pengamatan. Eksplorasi data merupakan bagian yang integral dari persepsi kita. Apabila tujuan akhir dari penelitian bukan untuk menghasilkan inferensi kausal, analisis data selanjutnya sudah tidak diperlukan lagi. Namun apabila diperlukan, analisis data eksploratori sangat menunjang dalam menelaah dan menemukan tentang sifat-sifat data yang nantinya dapat berguna dalam menyeleksi model statistik yang tepat. Dengan demikian, pada analisis data eksploratif, sifat dari data pengamatanlah yang akan menentukan model analisis statistik yang sesuai (atau perbaikan dari analisis yang sudah direncanakan).
Langkah pertama dalam menganalisis data adalah mempelajari karakteristik dari data tersebut. Terdapat beberapa alasan penting yang perlu kita pertimbangkan secara cermat sebelum analisis data sebenarnya kita lakukan. Alasan pertama pemeriksaan data adalah untuk memeriksa kesalahan-kesalahan yang mungkin terjadi pada berbagai tahap, mulai dari pencatatan data di lapangan sampai pada entry data pada komputer. Alasan berikutnya adalah untuk tujuan eksplorasi data sehingga kita bisa menentukan model analisis yang tepat.
- Dilihat: 15783
- Detail
- Ditulis oleh Ade Setiawan
- Kategori: Statisika Deskriptif
Rata-rata dan ukuran penyebaran dapat menggambarkan distribusi data tetapi tidak cukup untuk menggambarkan sifat distribusi. Untuk dapat menggambarkan karakteristik dari suatu distribusi data, kita menggunakan konsep-konsep lain yang dikenal sebagai kemiringan (skewness) dan keruncingan (kurtosis).
- Dilihat: 107939

- Detail
- Ditulis oleh Ade Setiawan
- Kategori: Analisis Data Eksploratif
Penyajian lain yang mirip dengan histogram adalah Stemplot. Stemplot juga dikenal sebagai stem-and-leaf plot atau apabila diterjemahkan ke dalam bahasa indonesia berarti plot batang dan daun. Di dalam statistik, stemplot merupakan alat untuk menyajikan data kuantitatif dalam format grafis, mirip dengan histogram, yaitu untuk membantu dalam memvisualisasikan bentuk distribusi data yang sering digunakan dalam analisis eksplorasi.
Stemplot diperkenalkan oleh Arthur Bowley di awal tahun 1900-an. Namun penggunaannya secara umum baru dimulai pada tahun 1980 setelah John Tukey's mempublikasikan Exploratory Data Analysis pada tahun 1977. Stem-and-leaf plot memberikan informasi lebih banyak tentang nilai yang sebenarnya dibanding histogram. Seperti dalam histogram, panjang setiap batang sesuai dengan jumlah kejadian yang jatuh ke dalam interval tertentu. Pada Histogram. kita hanya bisa melihat nilai frekuensi dari data namun kita tidak tahu berapa nilai angka sebenarnya. Berbeda dengan histogram, pada Stem-and-leaf plot selain kita bisa mengetahui nilai frekuensinya, kita pun bisa tau berapa nilai data sebenarnya. Hal ini dilakukan dengan membagi nilai-nilai yang diamati menjadi dua komponen, stem dan leaf.
- Dilihat: 14547
- Detail
- Ditulis oleh Ade Setiawan
- Kategori: Statisika Deskriptif
Distribusi Frekuensi adalah daftar nilai data (bisa nilai individual atau nilai data yang sudah dikelompokkan ke dalam selang interval tertentu) yang disertai dengan nilai frekuensi yang sesuai.
Hasil pengukuran yang kita peroleh disebut dengan data mentah. Besarnya hasil pengukuran yang kita peroleh biasanya bervariasi. Apabila kita perhatikan data mentah tersebut, sangatlah sulit bagi kita untuk menarik kesimpulan yang berarti. Data mentah tersebut perlu di olah terlebih dahulu sehingga kita bisa memperoleh gambaran yang baik mengenai data tersebut.
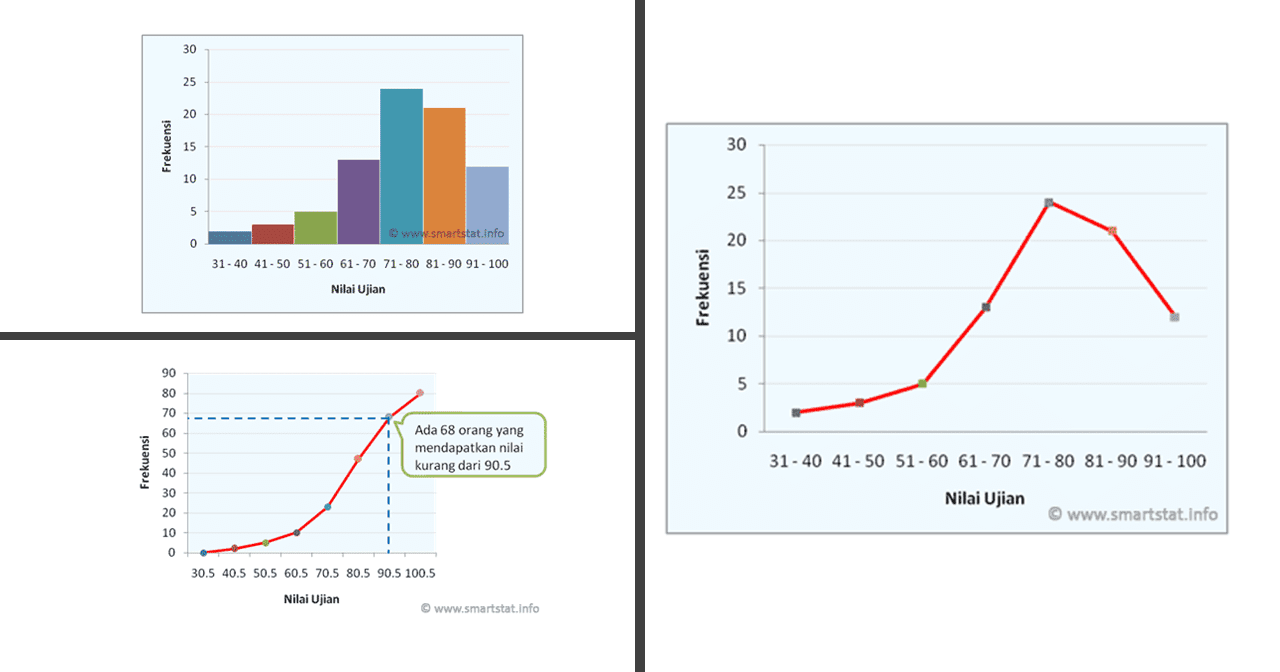
Pada bahasan kali ini, smartstat akan menguraikan mengenai pengertian distribusi frekuensi yang disertai dengan contoh dan Teknik Pembuatan Tabel Distribusi Frekuensi. Selain itu, akan dibahas juga mengenai Distribusi Frekuensi Relatif dan Distribusi Frekuensi kumulatif, Histogram, Poligon Frekuensi, dan Ogive.
- Dilihat: 173391

- Detail
- Ditulis oleh Ade Setiawan
- Kategori: Analisis Data Eksploratif
Baik histogram dan stem-and-leaf plots berguna untuk memberikan gambaran ukuran tendensi sentral dan kesimetrisan data pengamatan. Penyajian grafis lainnya yang bisa merangkum informasi lebih detail mengenai distribusi nilai-nilai data pengamatan adalah Box and Whisker Plots atau lebih sering disebut dengan BoxPlot atau Box-Plot (kotak-plot) saja. Seperti namanya, Box and Whisker, bentuknya terdiri dari Box (kotak) dan whisker.
Box-Plot merupakan ringkasan distribusi sampel yang disajikan secara grafis yang bisa menggambarkan bentuk distribusi data (skewness), ukuran tendensi sentral dan ukuran penyebaran (keragaman) data pengamatan.
Pada artikel Mengenal Box-Plot (Box and Whisker Plots) ini akan diuraikan secara rinci mengenai manfaat Box-Plot dalam menjelaskan ukuran tendensi sentral serta rincian detail bagian-bagian dari Box-Plot.
- Dilihat: 23874
Artikel Selanjutnya...
- Korelasi Pearson: Memahami dan Menggunakan dalam Analisis Data Statistika
- Regresi Linier Sederhana: Panduan Lengkap Untuk Pemula dalam Statistika
- Uji-t Student: Memahami dan Menggunakan dalam Analisis Data Statistika
- Uji-t Student Satu Sampel: Memahami dan Menggunakan dalam Analisis Data Statistika
- Uji-t Student 2 Populasi dengan Ragam Homogen: Memahami dan Menggunakan dalam Analisis Data Statistika
- Uji-t Student 2 Populasi dengan Ragam Heterogen: Memahami dan Menggunakan dalam Analisis Data Statistika
- Uji-t Student Berpasangan: Memahami dan Menggunakan dalam Analisis Data Statistika
- Uji McNemar: Contoh perhitungan dalam Analisis Data Statistika
- Uji Wilcoxon Untuk Data Berpasangan
- Tabel Distribusi Statistik: Memahami Nilai Kritis dalam Analisis Statistik
Halaman 2 dari 4

